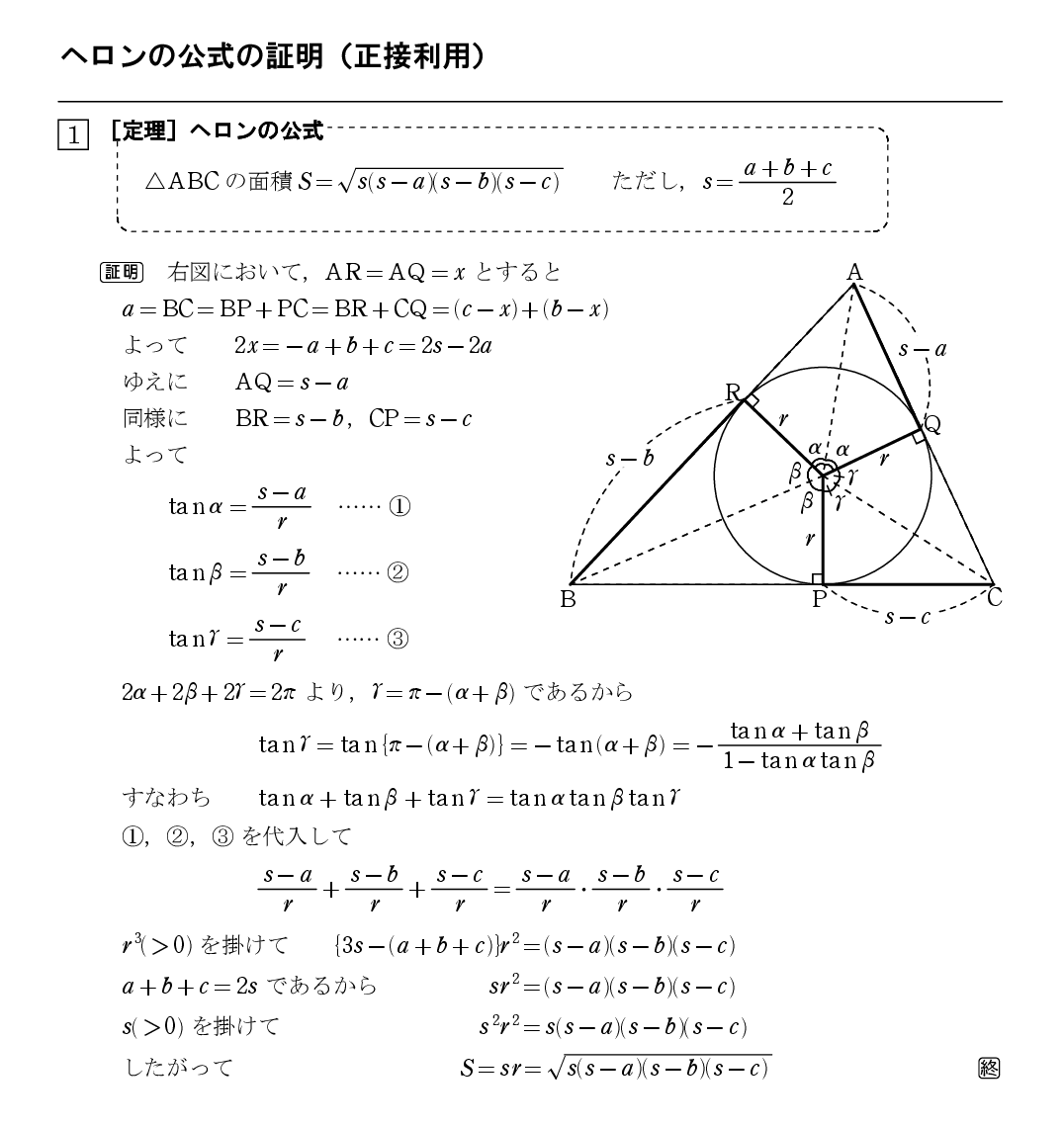
ナポレオンの定理は、フランスの皇帝ナポレオンが自ら見つけた定理と言われています。 余弦・正弦定理や加法定理を使い、計算によって証明してみました。 ①ナポレオンの定理とは 18世紀末の革命後、フランスの皇帝になったナポレオンは数学好きで才能も優れていたと言われています。ヘロンの公式の図解 Step① 内接円の性質から S = s r Step② s − a, s − b, s − c を見つける Step③ A P ′ = s を示す Step④ A P O と A P ′ O の相似 Step⑤ C O P と O ′ C P ′ の相似 Step⑥ (1), (2), (3) を解く 三角関数を用いた証明キーワード:ヘロンの公式,因数定理,同次多項式,逆問題 1.序 ― 美しいヘロンの公式とは 平面幾何学にヘロン( Heron )の公式という著名な定理がある. これは三角形の 3 辺の長さからその面積を求める大変綺麗な公式である. ABC の角A,
ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典
ヘロンの公式 証明 余弦定理
ヘロンの公式 証明 余弦定理-3辺の長さから三角形の面積を求める公式です。 中学生から高校生まで、知っていると非常に便利な計算方法です。 ①ヘロンの公式と名前の由来 ②証明(中3レベル) ③証明(数Ⅰレベル) ①ヘロンの公式と名前の由来 ヘロンの公式 3辺の長さが $~a ,b,,c~$ の三角形がある。ヘロンの公式 ただし、sは、三角形の周の長さの半分。 余弦定理と、例1.の公式を用いて示される。ただ少しばかり、因数分解が大変かもしれ ない。 例6.(例5.を初等的に導入)



1
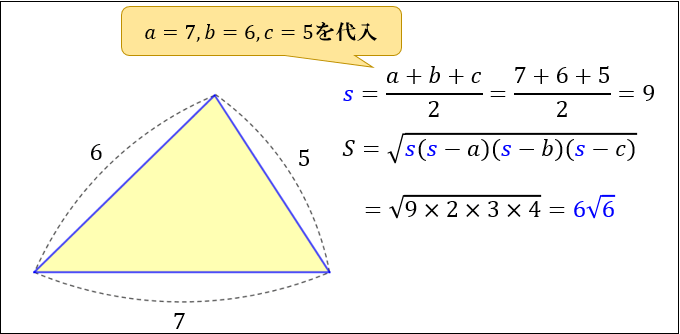
余弦定理の公式覚え方はどうする? 余弦定理の証明簡単にわかりやすく考えてみよう! 三角比 3分で理解!ヘロンの公式の使い方をイチからていねいに解説!これを一般化したものは、「ヘロンの公式」と呼ばれています。 まず、余弦定理から、次のことがわかります。 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9 式の計算 30 二項定理 14 等式と不等式の証明 33 複素数と方程式 35 図形と方程式 53 軌跡(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。
ヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a , b , c の長さから 面積S を求める公式である。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。 ただし, この証明には教材を概観することである。考察の対象は三角関数の加法定理,加法定理と2次元数, 余弦定理・正弦定理, トレミーの定理,ヘロンの公式,チェバの定理,メネラウスの定 理である。これらの結果をなるべく余弦・正弦定理を基にして証明する。lこの公式を用いて、ヘロンの公式を証明します。 まず、余弦定理により、 $$\cos{A}=\frac{b^2c^2a^2}{2bc}$$ となります。 余弦定理については、下の記事に詳しくまとめ
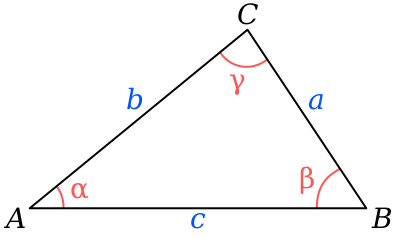
高校数学I ギリシア文字について 24 種類あるギリシア文字のうち,背景が灰色である文字は,数学I で用いられることがある. 英語 読み方 大文字 小文字 英語 読み方 大文字 小文字 alpha アルファ A nu ニュー N beta ベータ B xi クシー,グサイ ˘ gamma ガンマ omicron オミクロン O o6面積の公式からの証明 7第2余弦定理からの証明 1) 角B、Cについても同様の結果になることによって証明できる。またこの式の最右辺 に注目すると、外接円の半径Rをabcで表していたり、。ヘロンの公式が見えて興味深い三角形の形状問題も,角度に関する式を辺に関する式に直してから考えるのが基本です. a=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90°




3辺の長さが与えられたときの三角形の面積 中学 高校数学 身勝手な主張




ヘロンの公式 を使って面積を求める方法 証明あり ますますmathが好きになる 魔法の数学ノート
数学Ⅰ1数と式 展開公式・因数分解公式α 絶対値の性質・方程式・不等式 平方根の性質・2重根号22次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3図形と計量 正弦定理・余弦定理 $90^{ \ヘロンの公式を三平方の定理から導く 3辺の長さがa,b,cであるような ABCの面積Sは、2t=abcとおくと、次式で求まる。 となる。 証明1三角関数を使うものがよく知られている。 証明2三平方の定理でも証明できる。 3辺のうち最も長いのが辺ABであるとし7 第2余弦定理からの証明 1) 角B、Cについても同様の結果になることによって証明できる。 またこの式の最右辺に注目すると、外接円の半径Rをabcで表していたり、ヘロンの公式が見えて興味深い。



高校数学 Net




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
余弦定理とは何か? 図解でわかるその使い道と公式の証明 とおいたときに、 以下の3つの式が成り立つことを余弦定理 と言います。 余弦定理は、「2辺の長さとその間の角度」から「残り1辺の長さ」を求めたり、「3辺の長さ」から「3つの角度」を求める余弦定理はピタゴラスの定理を使って証明されるものと聞きましたが、ヘロンの公式は余弦定理を使って証明できるものでしょうか。余興の尻ぬぐいですが。>これを (1) か (2) へ代入して、h^2 が (したがって h も) 求まる。>h がわかるの内積 * 外積 # 10^x=Ten(x) 微分 ;x 時間微分 ' 積分 $ ネイピア数 e e^x=exp(x) i^2=1 e^(i*x)=exp(i*x)=expi(x) 〓 余




ヘロンの公式の証明 導出 を徹底解説 5分でわかる Youtube



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ
ピックの定理に戻る 卒業研究 TOP ヘロンの公式 三角形の面積を求めるときに用いたヘロンの公式を紹介します。 <証明> 使用する公式 ・三角関数の基本公式 sin 2 Acos 2 A=1 ・余弦定理 a 2 =b 2 c 22bccosA b 2 =c 2 a 22cacosB c 2 =a 2 b 22abcosC余弦定理の公式を証明 – 図を使って丁寧に説明 しかし、ある条件が揃っている場合、ヘロンの公式を使った方が格段に早く面積を求めれます。 その条件とは、 面積を求めたい三角形の三辺の長さがすべてわかっている場合 です。★ 三角形の辺の長さと角に関する定理 余弦cos 正弦sin ヘロンの公式 ベクトル <A>



ヘロンの公式 三辺から面積を求める をシミュレーターを使って理解しよう 数学入門
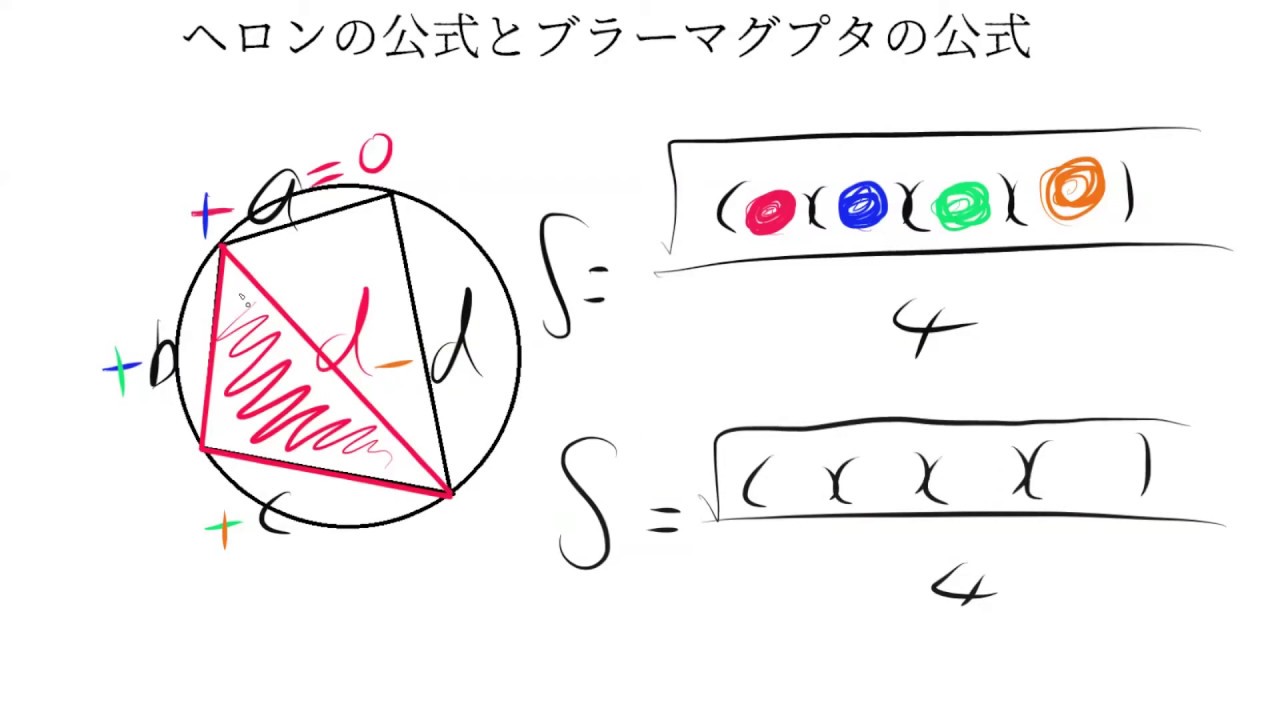



ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube
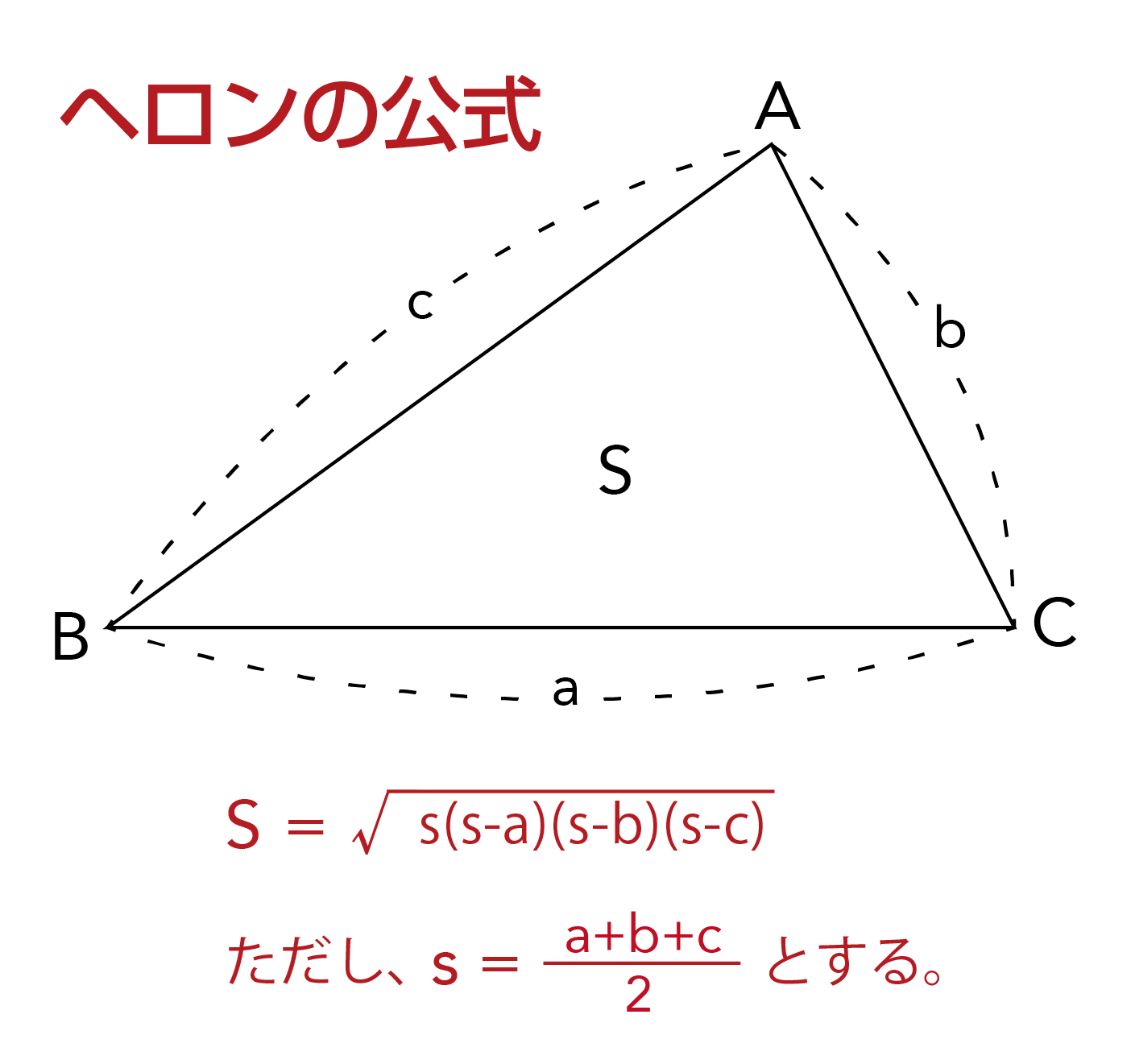
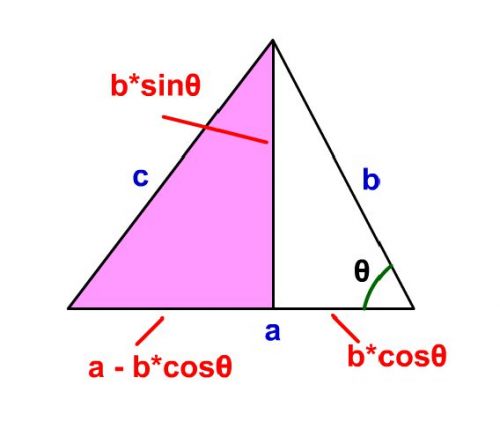
1 ヘロンの公式とは 2 ヘロンの公式の証明 21 三角形の面積は「底辺×高さ÷2」で求められる 22 三角形の高さは「斜辺×sinθ」で求められる (cos/sinの活用) 23 cosθは三辺の長さから求められる (余弦定理) 24 sinθは定理を使えば簡単にcosθに変換できる 25MathAquarium定理・公式の証明三角形の面積(ヘロンの公式) 1 三角形の面積 ABC において,頂点A,B,C における角の大きさ をA,B,C,その対辺BC,CA,AB の長さをそれぞれ a,b,c,面積をS とすると,次の等式が成り立つ。 S= 2 1 bc sinA= 2 1 ca sinB= 2 1 abヘロンの公式 三角形 ABC A B C の面積を S S とすると, s = ab c 2 s = a b c 2 として, S = √s(s −a)(s−b)(s −c) S = s ( s − a) ( s − b) ( s − c) 証明 三角形 ABC A B C に対して,余弦定理を用いると c2 = a2 b2 −2abcosC ⇔ cosC = a2 b2 −c2 2ab c 2




5講 三角形の内接円と面積 3章 2節 三角形の応用 問題集 高校数学
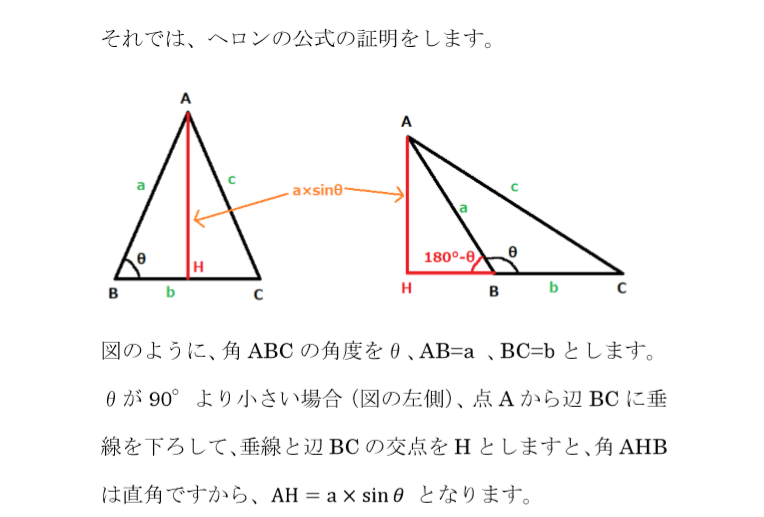



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
と、証明できました 中学数学の知識で証明する 中学数学では、三角関数や余弦定理について学ばないので、これらを使わずに証明していきます 三角形abcの頂点aから線分bcに垂線を下ろし、交点をhとします ah = h , bh = dとおきます数学 ヘロンの公式は余弦定理から導かれますか 余弦定理はピタゴラスの定理を使って証明されるものと聞きましたが、ヘロンの公式は余弦定理を使って証明できるものでしょうか。 質問Noヘロンの公式の証明 辺の長さが である2辺の間の角を とします。 三角比を用いた三角形の面積 より、 (1) 余弦定理 より、 (2) 三角比の相互関係式 より、 (3) (2)式を (3)式に代入する
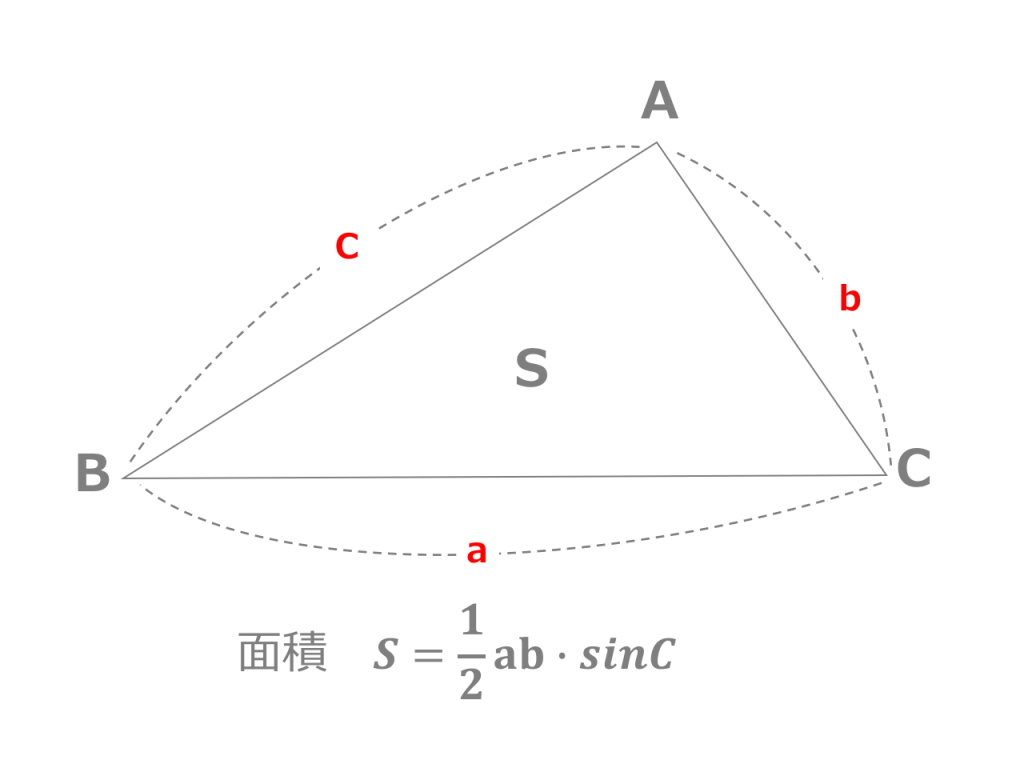



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ



3




ヘロンの公式 Wikipedia



1




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



ヘロンの公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




ヘロンの公式




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト




三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




最高 ヘロン の 公式 証明 トップイラスト



1




ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ
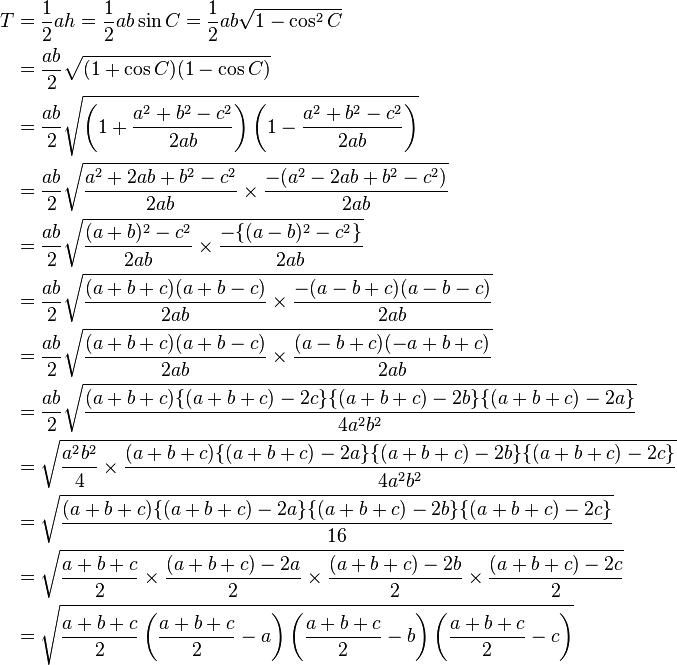



ヘロンの公式の証明 三角関数を使わずに ようこそ なるのホームページへ



カルダノ




ブラーマグプタの公式 ヘロンの公式と証明



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典
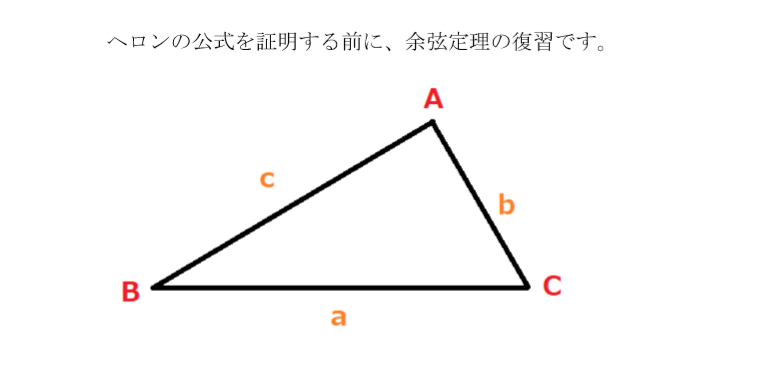



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ




ヘロンの公式の余弦定理による証明と幾何的な証明 図形についての新しい探求 Mathtematics For Teachers




3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ



ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
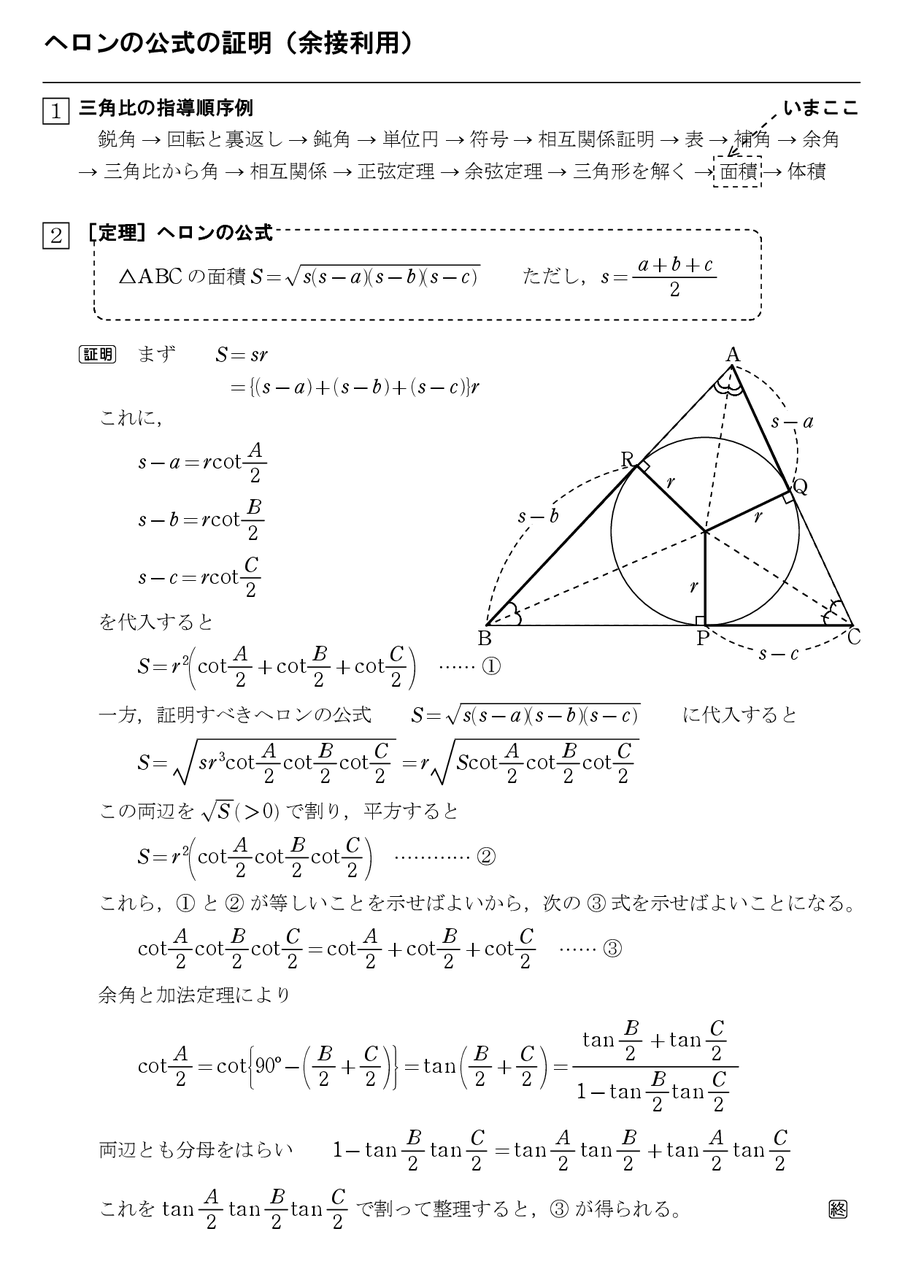



ヘロンの公式の証明 余接利用 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式の証明と使用例 高校数学の美しい物語




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月




ヘロンの公式 Wikipedia




15年08月 怜悧玲瓏 高校数学を天空から俯瞰する




ヘロンの公式 三角形の面積 大学入試数学の考え方と解法




ヘロンの公式 東大合格コム




ヘロンの公式



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




ヘロンの公式の導き方 直ぐには分からなかった さんの日記 50代から理数を学ぶ



ヘロンの公式 思考力を鍛える数学
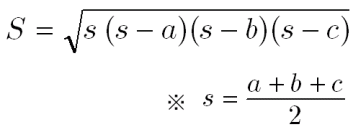



三角比 ヘロンの公式 を導く 大人が学び直す数学




山と数学 そして英語 三平方の定理と三角形の面積 さらに三角比 ヘロンの公式
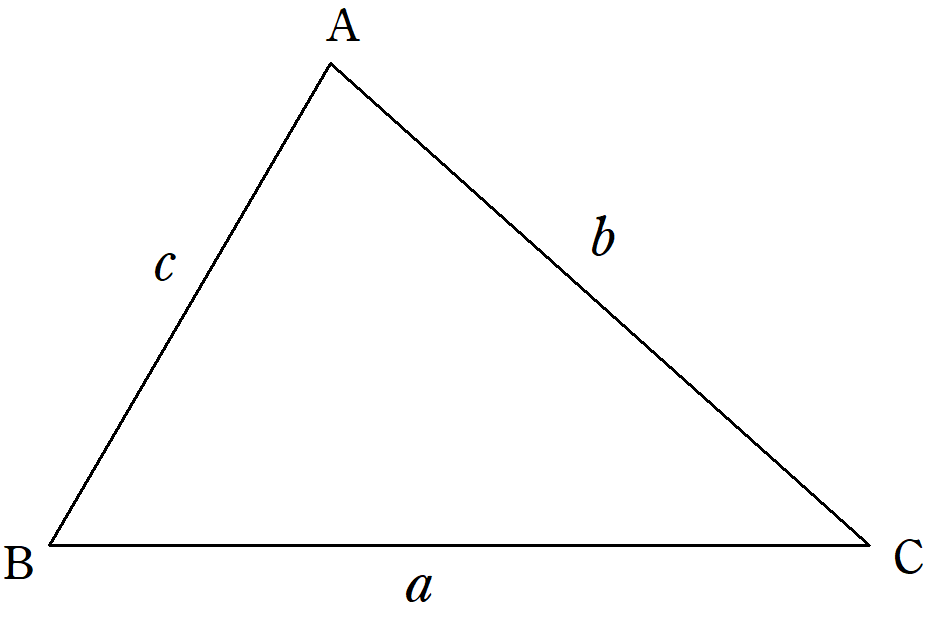



ヘロンの公式 Fukusukeの数学めも




ヘロンの公式 導出と計算例



高校数学 Net




ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




ヘロンの公式とは ヘロンノコウシキとは 単語記事 ニコニコ大百科




高校数一 ヘロンの公式 を使いこなそう 三角形の面積の求め方のまとめ ジルのブログ



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門



ヘロンの公式 Fukusukeの数学めも




最も欲しかった ヘロン の 公式 証明 ヘロンの公式 証明 簡単 Blogjpmbahewpme




ヘロンの公式の証明と例題 数学i By ふぇるまー マナペディア



ヘロンの公式 Hero S Formula




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



最高 ヘロン の 公式 証明 100以上の最高の絵のゲーム




高校生 ヘロンの公式のノート一覧 Clearnote




高校生 ヘロンの公式のノート一覧 Clearnote




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri
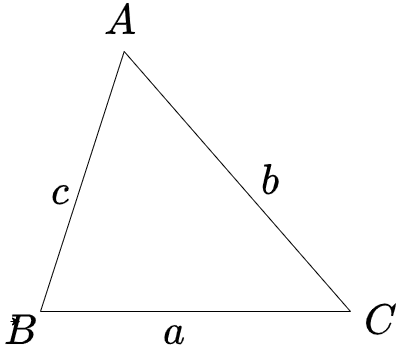



中学数学で出来る ヘロンの公式の証明




余弦定理の証明 高校生 数学のノート Clearnote




Haruka先生の数学証明シリーズ ヘロンの公式 Youtube
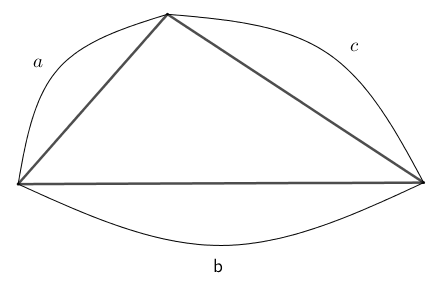



ヘロンの公式の証明 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




ヘロンの公式のスモールsってどういう意味でしょうか 誰か教えてくださいm M 基塾長の成績の上がるブログ




3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ



この数学の問題を ヘロンの公式を使わずに 三平方の定理での解き方を教え Yahoo 知恵袋




最高 ヘロン の 公式 証明 トップイラスト
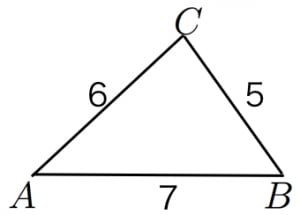



ヘロンの公式の証明と使用例 高校数学の美しい物語




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
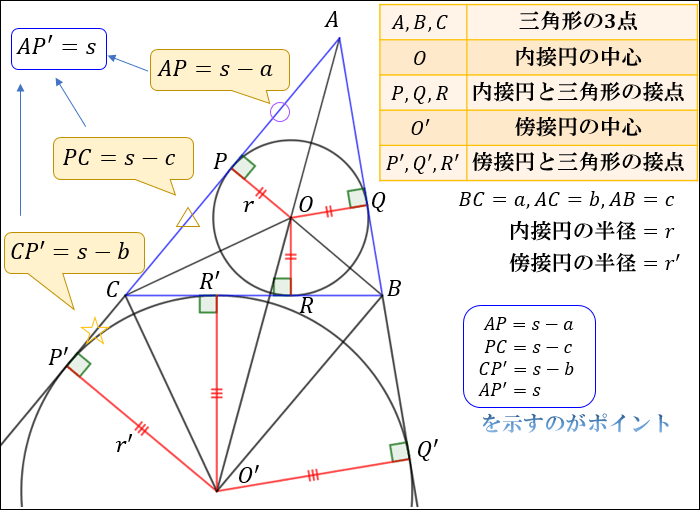



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



ヘロンの公式 Wikiwand
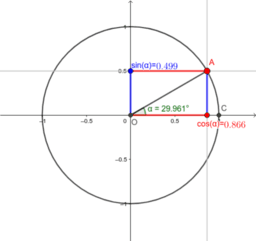



三角関数の公式 Geogebra



後藤信行 Jp




ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ




ヘロンの公式




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月
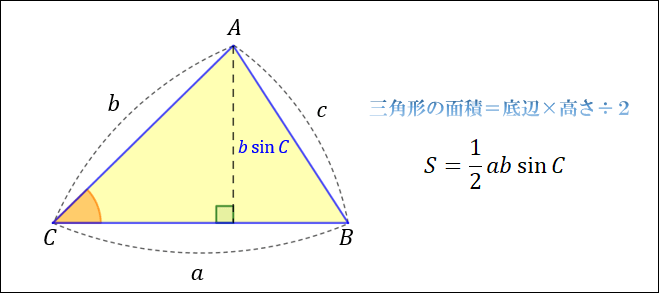



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




美しい公式 ヘロンの公式は 共通テストで狙われるかも でもそうでないとしてもこれは簡単すぎて美しすぎる公式だと思います 学習村の 国公立へ行こう
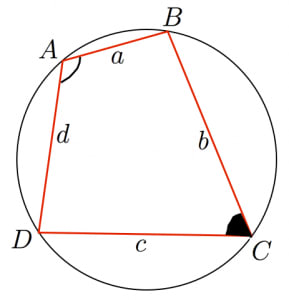



ブラーマグプタの公式とその2通りの証明 高校数学の美しい物語




ブラーマグプタの公式 17年 大阪教育大 数学日和
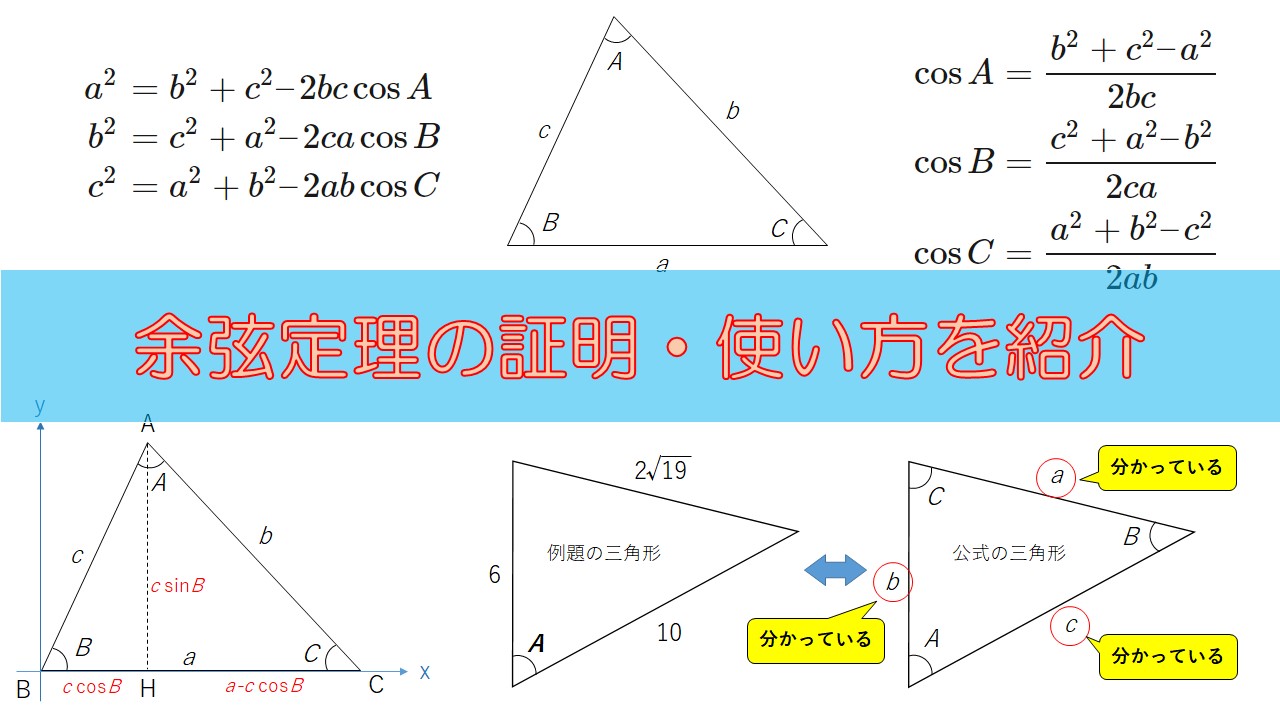



高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト
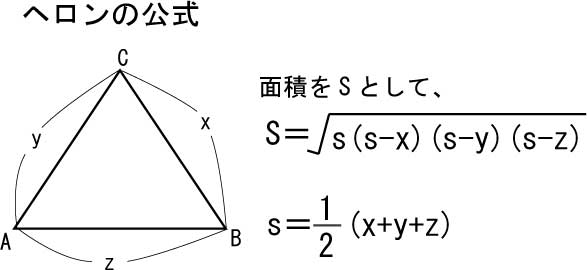



正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー




ヘロンの公式 三辺から面積を求める をシミュレーターを使って理解しよう 数学入門
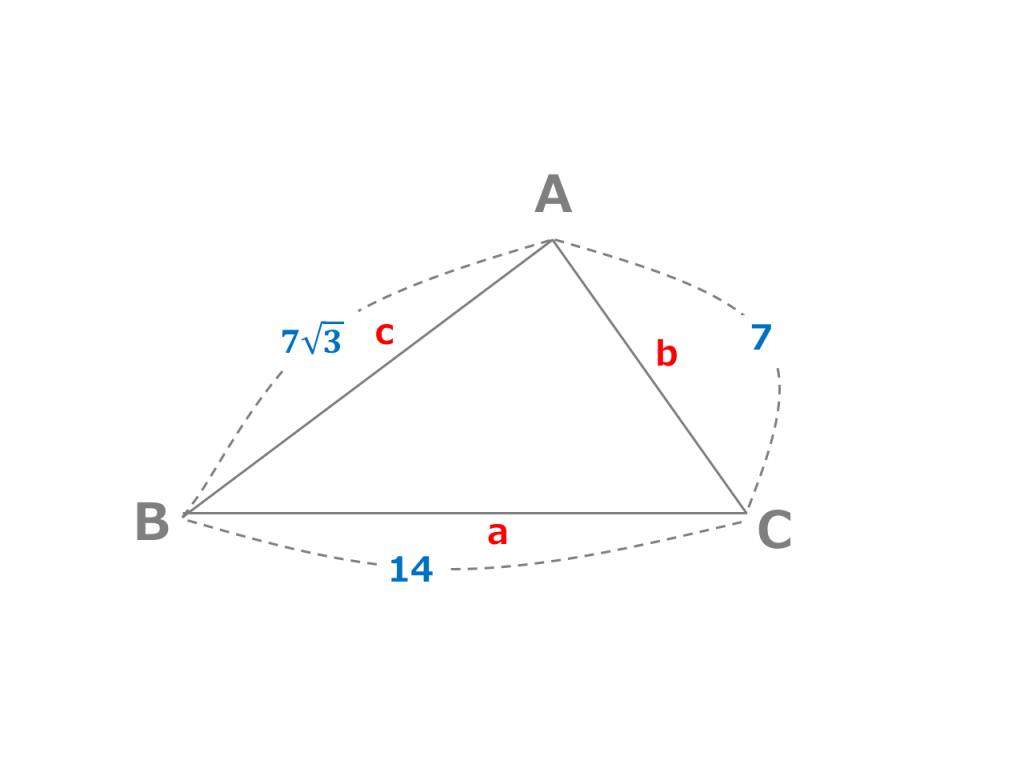



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ
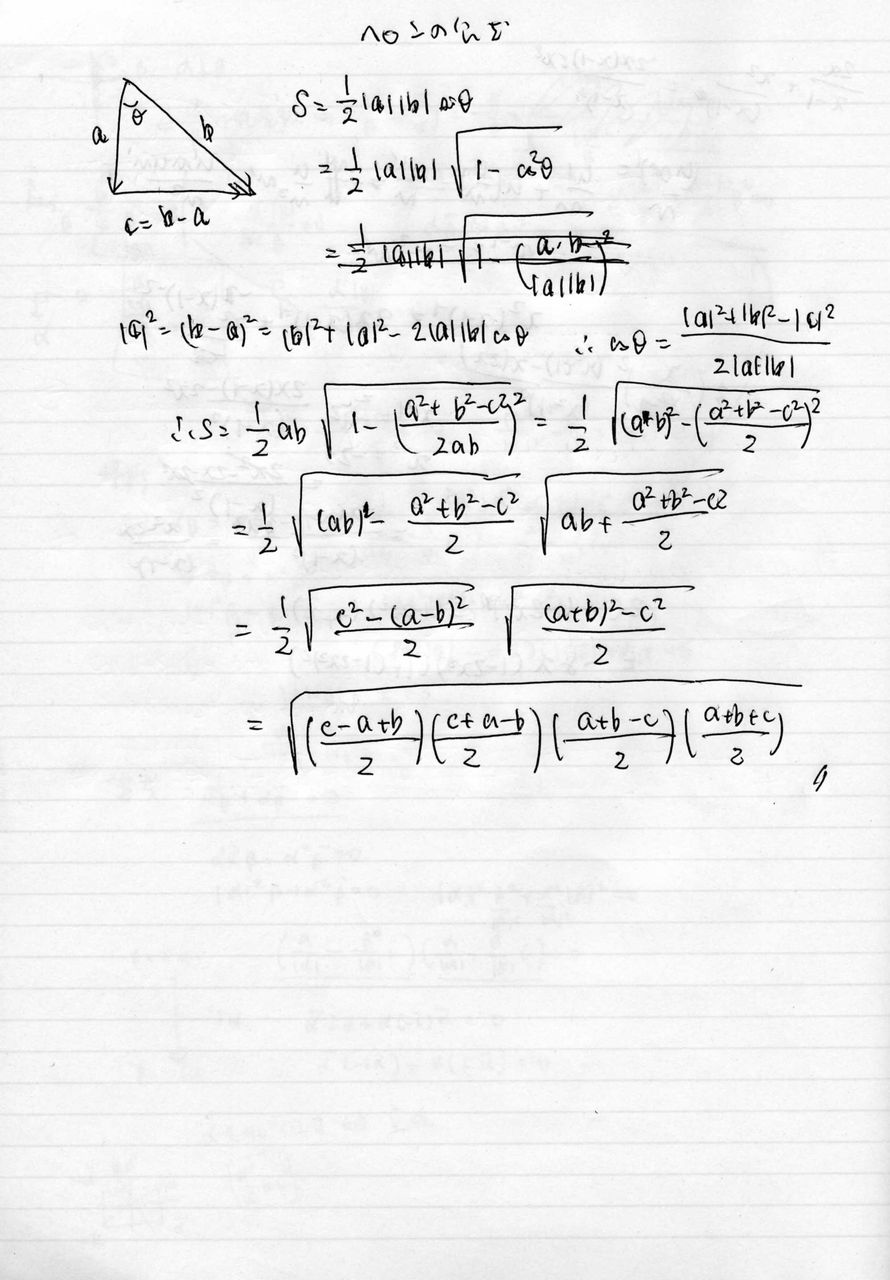



ヘロンの公式 東大合格コム




人気の ヘロンの公式 動画 2本 ニコニコ動画




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri




5講 三角形の内接円と面積 3章 2節 三角形の応用 問題集 高校数学




重心の存在証明とヘロンの公式の証明 大阪教育大学10年後期数学第2問 理系のための備忘録




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ



1
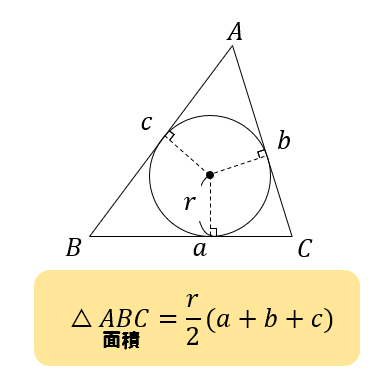



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ
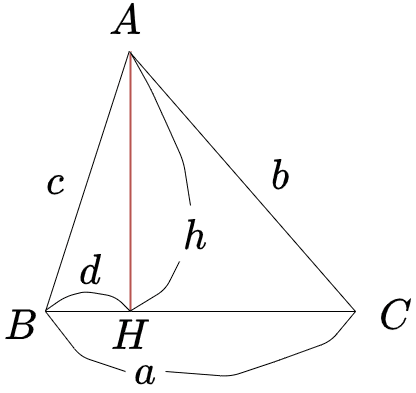



中学数学で出来る ヘロンの公式の証明
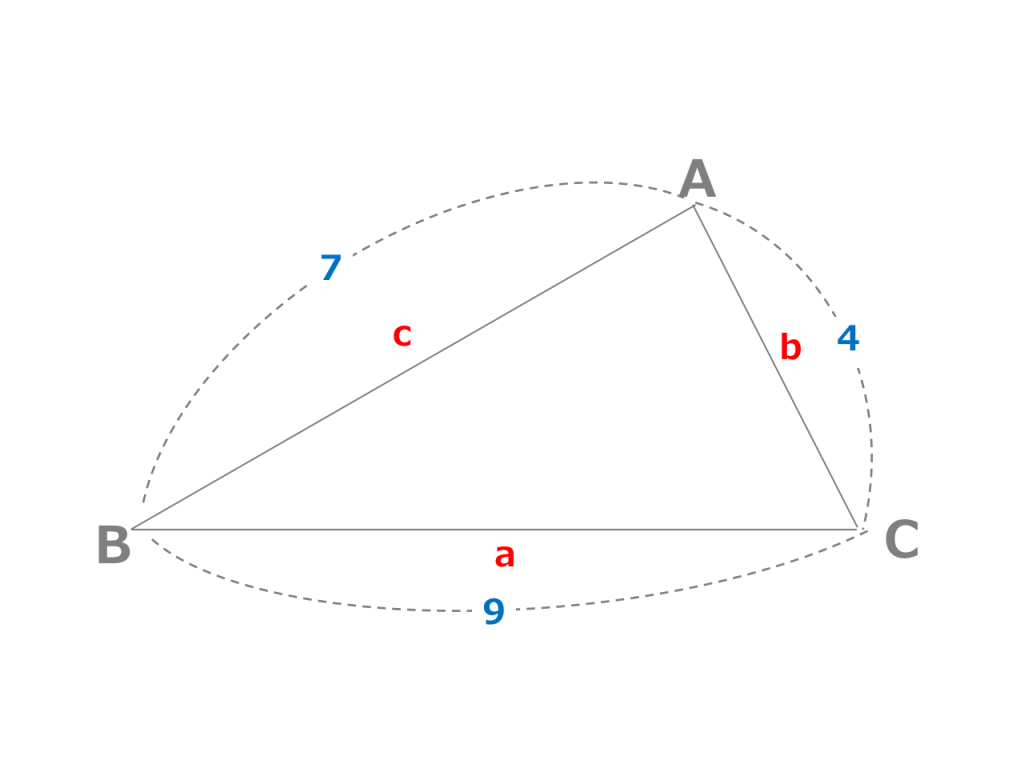



3分で分かる ヘロンの公式 証明と問題の解き方をわかりやすく 合格サプリ



ヘロンの公式の部屋




ヘロンの公式の証明と使用例 高校数学の美しい物語
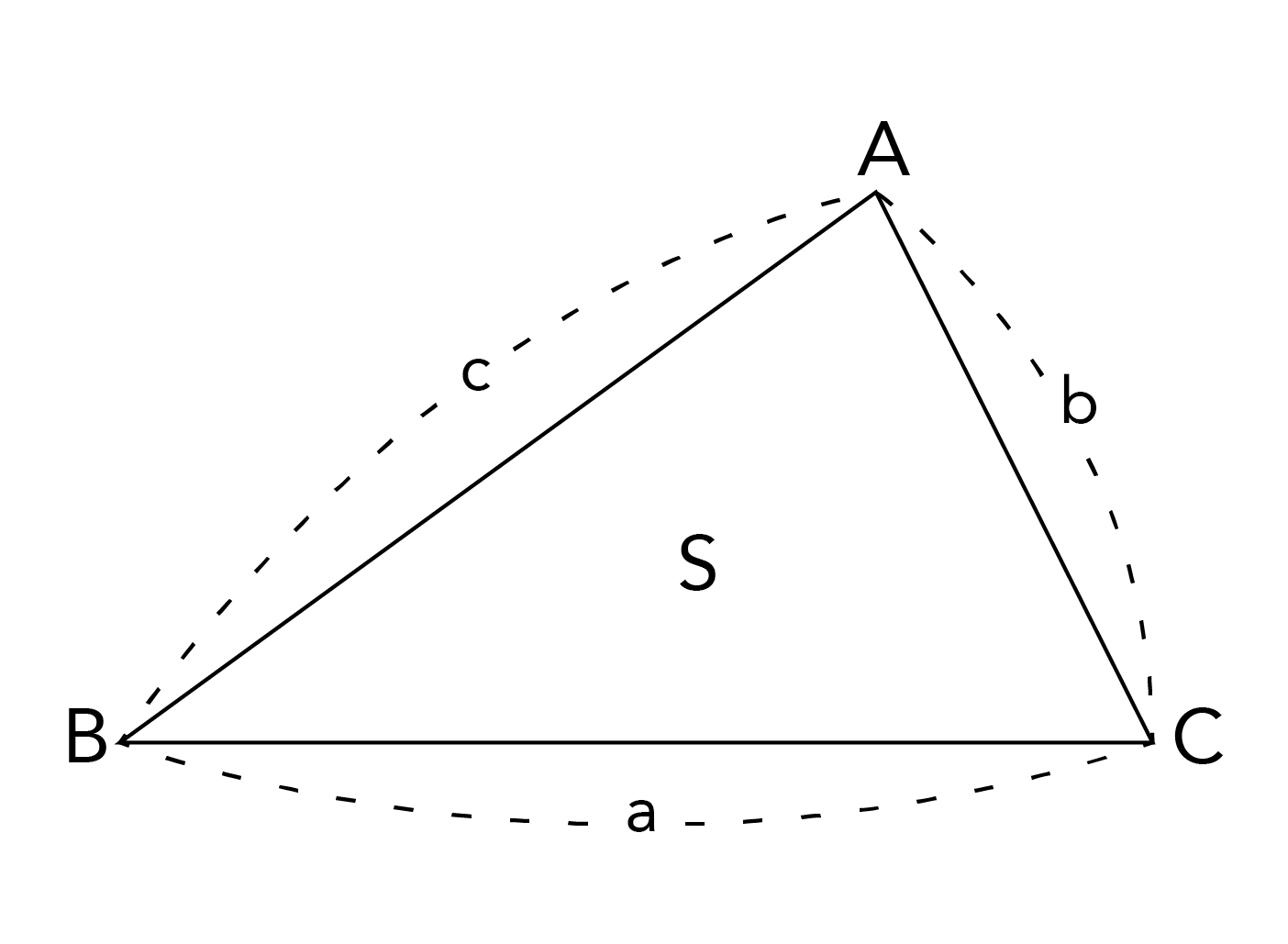



ヘロンの公式が一目でわかる 見やすい図で慶應生が解説 高校生向け受験応援メディア 受験のミカタ
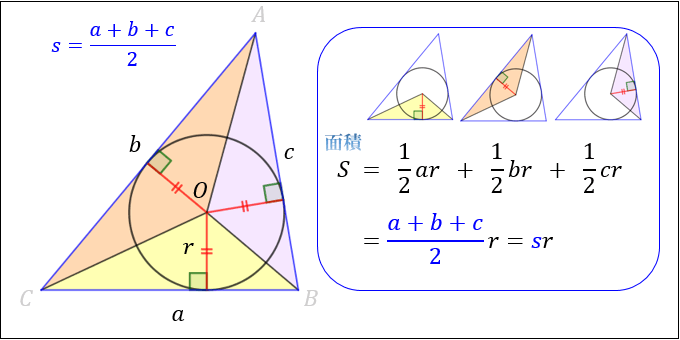



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



0 件のコメント:
コメントを投稿